- ホーム
- <ショートサービス研究室>理想的なショートサービスの軌道とは?
<2021/9/17公開>
ネットの上ぎりぎりを通過し、ネットを越えたとたん急に方向を変え、減速することなくショートサービスラインへ向かって一直線に飛んでいく。
こんなサーブが打てれば無敵ですが、実際には無理ですよね。
浮かない理想的なサービスを打てた時、シャトルはどんな軌道を描いているのでしょう?
地球上にいる限り、どんなものも、重力による自然落下と空気抵抗による減速を免れることはできません。
ショートサービスに限らず、ラケットから放たれたシャトルは、物理法則に従い、放物線に近い軌道で飛んでいきます。
ネットに当たりでもしない限り、急にシャトルの飛ぶ方向が変わることはあり得ません。
「放物線に近い」と表現したのは、シャトルは空気抵抗による減速の影響を受け、完全に左右対称の放物線にはならないからです。
ハイクリアを打った時の軌道をイメージしていただくと、わかりやすいと思います。
【ハイクリアの軌道】

ショートサービスでも、同じような軌道になるのでしょうか?
ショートサービスが苦手な方は、ひょっとすると、軌道の作り方に原因があるかもしれません。
この研究では、物理の根拠に基づいて、理想的なショートサービスの軌道を明らかにします。(と言っても、物理の計算式に頼らず、直感的にわかるように書いていますので、ご安心ください。)
<研究報告>
下図は、コートを横から見たものです。
ネットからショートサービスラインの中心までの距離はちょうど2mです。
ショートサービスはネットの中央付近を通過しますので、ネットの高さは1.524mとして考えます。
【ショートサービスラインぎりぎりに打つと軌道はどうなる?】
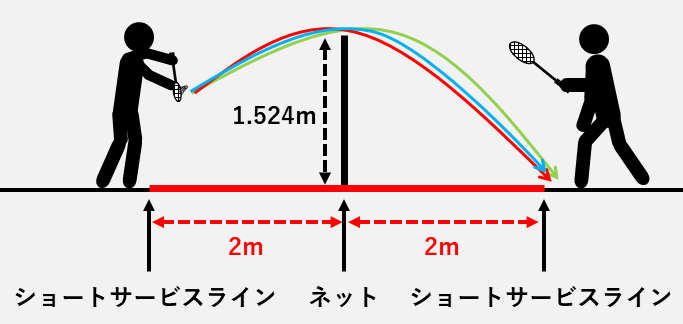
【軌道拡大図】
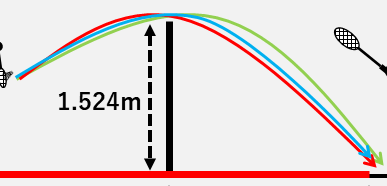
ネットの上すれすれを通して、ショートサービスラインぎりぎりに入るサーブを打つと、軌道の頂点は次の3つのうち、どこに来ると思いますか?
(1)ネットよりも手前側(赤の軌道)
(2)ネットの真上付近(青の軌道)
(3)ネットよりも向こう側(緑の軌道)
空気抵抗の影響をいったん無視すると、ラケットを離れた後シャトルに加わる力は重力(下向きの力)だけです。
横向きの力は働きませんので、シャトルは床と平行な方向には同じ速度で飛び続け、上下方向には重力による自然落下が起こります。
その結果、シャトルは左右対称の綺麗な放物線軌道を描きます。
サーバーの打点を、ショートサービスラインより20cmネット寄りかつ高さ110cmの打点とし、Excelを使って、グラフを描かせてみます。
ショートサービスラインぎりぎりに立ち、サービスフォルトにならないぎりぎりの高さでサービスする状況を想定して、この打点にしました。
もし、ネットの真上10cmに軌道の頂点が来るようにサーブすると、こんな軌道になります。

シャトルは相手ショートサービスラインより1m以上も先に着地します。
まだ空気抵抗を無視しているとは言え、思ったよりも飛ぶと思いませんか?
では、ネットの真上10cmを通過し、相手ショートサービスラインの先10cmのところに着地させようとすると、どうなるのでしょう?
理想的なショートサービスの軌道(空気抵抗を無視)
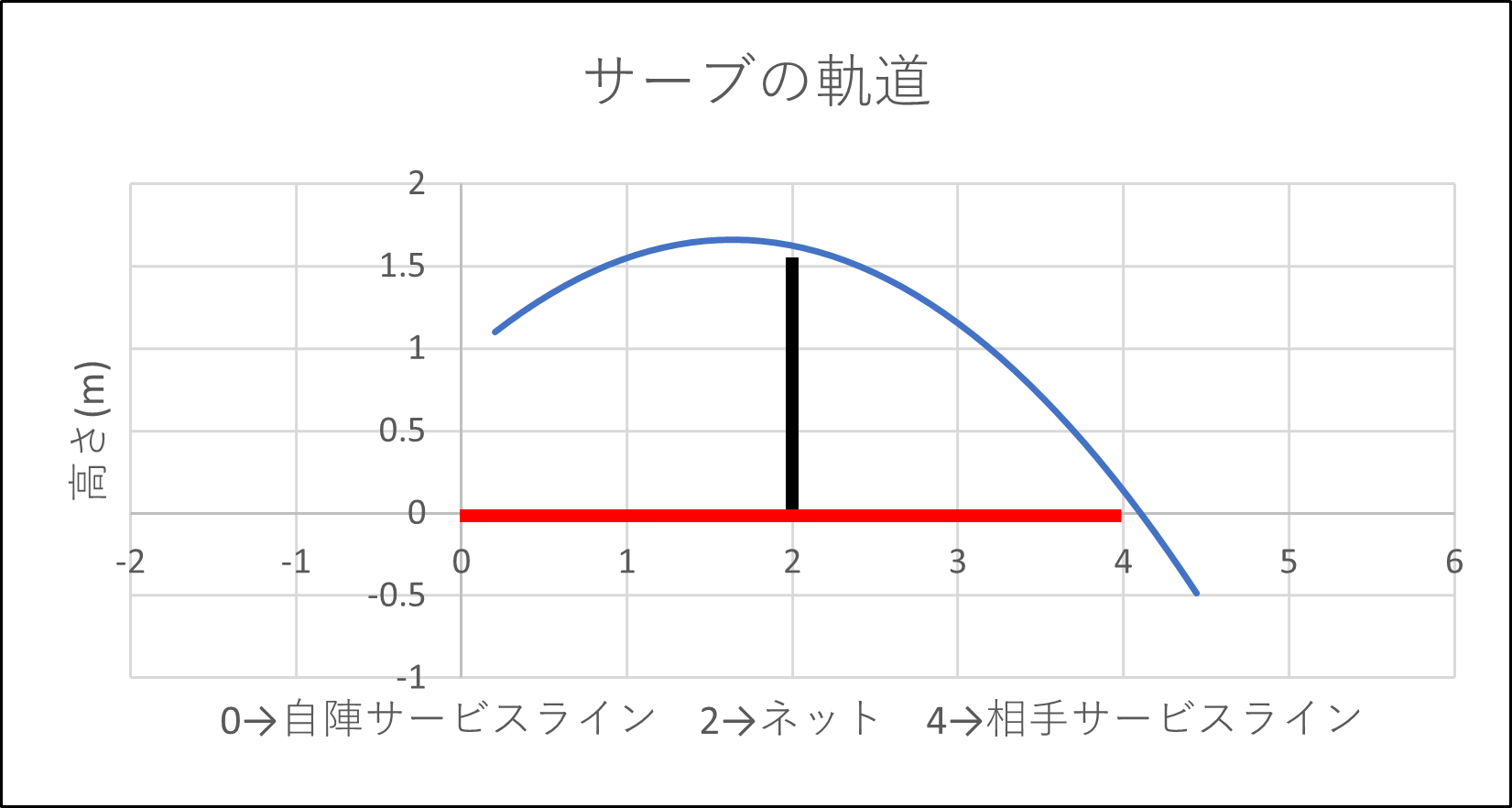
頂点の位置はネットの手前40cm程度のところに来ます。
まだ空気抵抗を無視していますが、頂点はネットよりも手前に来そうな感じがしてきましたね。
ここまでの解説で、こんな疑問を持たれた方がいるかもしれません。
ハイクリアの軌道は明らかに左右非対称で、空気抵抗による失速のために、軌道の頂点は相手のコート側に来ます。
ショートサービスでも同じことが起こるのではないでしょうか?
それでは、空気抵抗を考慮して、ショートサービスの軌道を計算してみましょう。
一般的に、空気抵抗の大きさは、物体の速度が遅い時は速度に比例し、速い時は速度の2乗に比例するとされています。
スマッシュやハイクリアの初速は、優に時速100kmを越えるため、速度の2乗に比例した空気抵抗を受けると考えられます。
これは、速いショットは、打ち出し直後とその後では、速度や軌道が大きく変わることを意味します。
だから、時速200km以上のスマッシュを打ち返せたり、ハイクリアが上から落ちて来るような軌道になったりする訳です。
一方、ショートサービスの初速は時速20km程度にしかなりません。
これくらいだと、空気抵抗の大きさは速度に比例すると考えても差し支えないでしょう。
ショートサービスでは、シャトルがスマッシュの時のように失速したり、ハイクリアの時のようにストンと落ちたりしないことを考えても、こう考えるのが妥当です。
残念ながら、空気抵抗が速度にどれくらい比例するのか、ほとんど研究データがなく、ショートサービスをターゲットにした研究に至っては皆無です。
そこで、大外れはしていないと思われる空気抵抗を設定して、Excelでグラフを描かせてみました。(空気抵抗がない時と比べ飛距離が10%程度落ちる抵抗条件にしています。)
空気抵抗を無視した場合と同様、ネットの真上10cmを通過し、相手ショートサービスラインの先10cmのところに着地させる軌道を描かせると、こうなります。
理想的なショートサービスの軌道(空気抵抗あり)

頂点の位置はネットの手前30cm程度のところに来ます。
空気抵抗を無視した場合と比べ、10cmほど頂点の位置がネット側へ近づくだけで、相変わらず軌道の頂点はネットよりも手前にあります。
つまり、ネットの上すれすれを通して、ショートラインぎりぎりに入るサーブを打つと、軌道の頂点はネットの手前側に来ます。
ネットの真上や向こう側に軌道の頂点を作ってしまうと、足の長いサーブになってしまい、相手コートのショートサービスラインぎりぎりには落とせないということになります。
ここでは、重力と空気抵抗の影響だけを考えましたが、打ち方によってはシャトルが不安定な動きをして、軌道に影響する可能性があります。
上級者の中には、コルクの向きをコントロールして、プッシュされにくくしようとする人もいます。
しかし、初中級の方にとっては、サービスが浮いたり、ショートしたりするリスクの方が大きいので、おすすめしません。
普通にサーブを打つ限り、シャトルの向きはすぐに安定しますので、打ち方による軌道への影響は無視してよいでしょう。
<結論>
物理の根拠に基づくと、空気抵抗を考慮してもしなくても、ネットよりも手前に軌道の頂点を作ることが、理想的な浮かないショートサービスの軌道だと言えます。
ネットを越えた直後から斜め下向きに飛び始めるのが、浮かないサービスだと思われていた方は多いかもしれませんが、物理の理屈では、ネットの少し手前から斜め下向きに飛び始めるのが、浮かないサービスだったのです。
<理想的な軌道を作るためのアドバイス>
ショートサービスを安定させるには、はっきりとした目標物があった方が楽です。
軌道の頂点をネットの手前に作ろうとしても、頂点付近には目標物がないため、安定したサーブを打つのは難しいかもしれません。
そこで、ネットの白帯とショートサービスラインを目標物にすることをおすすめします。
シャトルが、ネットの上10cmのところを通過して、相手サービスラインより10cm向こう側に着地するように打つことを目指しましょう。
このように打てると、意識しなくても軌道の頂点はネットより手前に来ます。
ミスするリスクを下げ、厳しくプッシュされるリスクも抑えるには、ぎりぎりを狙いすぎず、浮きすぎない軌道にすることが大切です。
サービスの軌道は、シャトルを打ち出す角度と強さで決まります。
まずは、強さを気にせず、ネットの上10cmを通過するように打ってみましょう。
相手のショートサービスラインより10cm先を基準にして、それより向こう側にシャトルが着地するなら、少し弱めに、手前側にシャトルが着地するなら、少し強めに打ってみましょう。
後は微調整していき、だいたい狙った通りに打てるようになってきたら、繰り返し練習して感覚を身につけましょう。
【参考】
<軌道計算に用いた運動方程式>
m*dvx/dt=-k*vx
m*dvy/dt=-k*vy-m*g
<計算結果>
vx=v0*cosθ*e(-k*t/m)
vy=(v0*sinθ+m*g/k)*e(-k*t/m)-m*g/k
x=m/k*(vx0-vx)+x0
y=m/k*(vy0-g*t-vy)+y0
vx0=v0*cosθ
vy0=v0*sinθ
ここで、
v(m/s):時刻t(s)におけるシャトルの速度
vx(m/s):時刻t(s)におけるシャトルの水平方向の速度成分
vy(m/s):時刻t(s)におけるシャトルの垂直向の速度成分
x(m):時刻t(s)における水平方向のシャトル位置
y(m):時刻t(s)における垂直方向のシャトル位置
v0(m/s):シャトルの打ち出し速度
vx0(m/s):シャトルの水平方向の打ち出し速度成分
vy0(m/s):シャトルの垂直方向の打ち出し速度成分
x0(m):水平方向のサービス打点(サービスラインからの距離)
y0(m):垂直方向のサービス打点(床からの距離)
θ(rad):シャトルの打ち出し角度
<定数>
m=0.005(kg):シャトルの質量
g=9.80665(m/s2):重力加速度
k=0.001(kg/s):空気抵抗係数
<次回研究予告>
では、サービスを厳しくプッシュされないためには、どこに立って、どれくらいの打点で打つのがよいのでしょう?
できるだけ前で高い打点から打った方がよいのでしょうか?
それとも、少し下がったところから速いサーブを打った方がよいのでしょうか?
これにも物理の根拠から導かれる答えがあります。
→本研究は、バド福LINE公式アカウントで週1回配信中の「ダブルスお役立ち情報」との連動企画です。この研究報告は、次回配信日2021/9/24に公開予定です。
ショートサービス研究室へ戻る







